The Framework
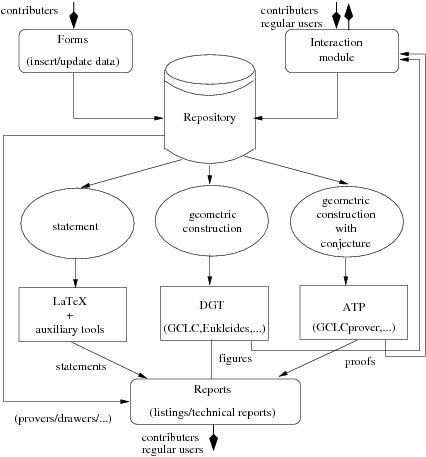
GeoThms, is a framework that link dynamic geometry tools (GCLC,
Eukleides), geometry automatic theorem provers (GCLCprover), and a
repository of geometry problems (geoDB) (see Figure
).
GeoThms provides a Web workbench in the field of constructive problems
in Euclidean geometry. Its tight integration with dynamic geometry
tools and automatic theorem provers (GCLC [DJ04][JT03],
Eukleides [Obr][QP06], and
GCLCprover [QJ06], for the moment) and its repository of
theorems, figures and proofs, give the user the possibility to easily
browse through the list of geometric problems, their statements,
illustrations and proofs, and also to interactively use the drawing
and automatic proof tools.
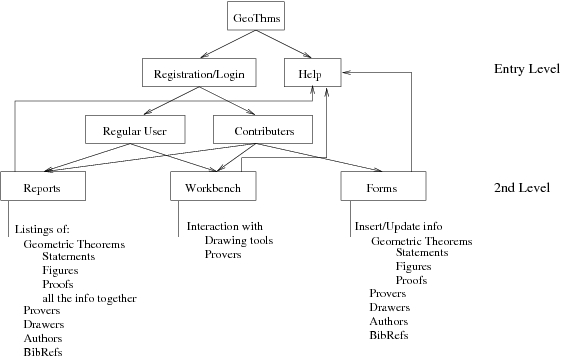
The structure of the web interface has two main levels of interaction
(see Figure ).
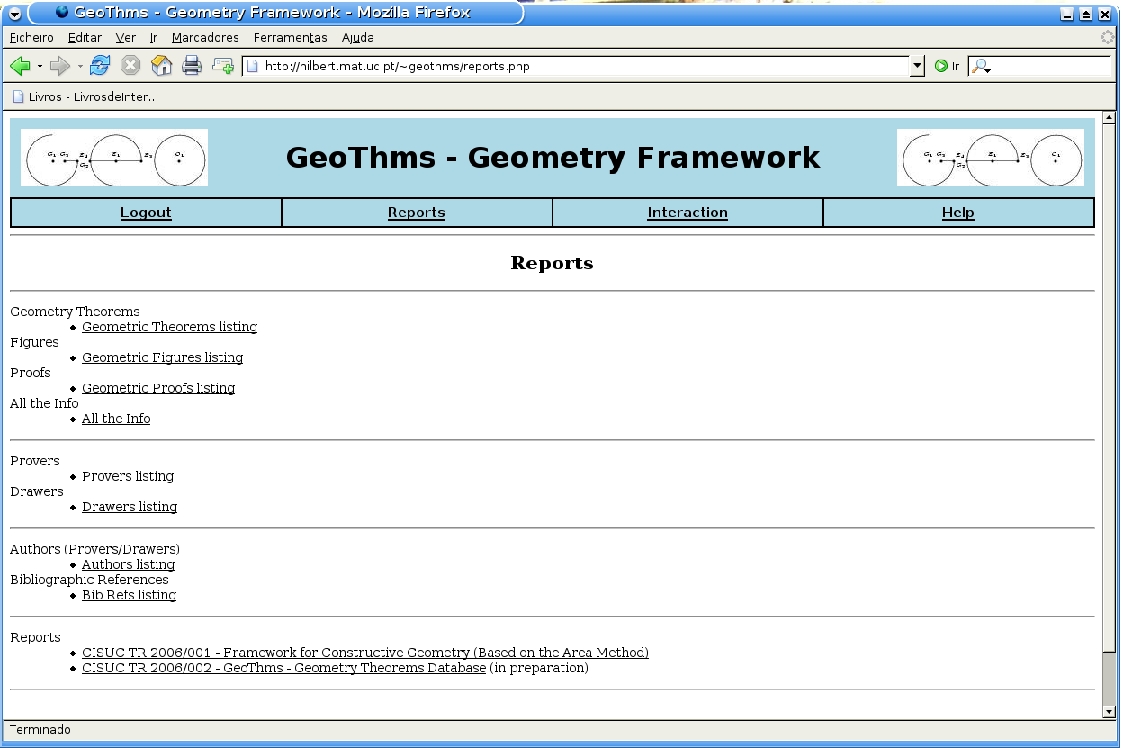
The entry level (see Figure ), accessible to
all web-users, has some basic information about GeoThms, offers the
possibility of registration to anyone interested in using GeoThms, and
it gives access to the other levels. A (registered) regular user has
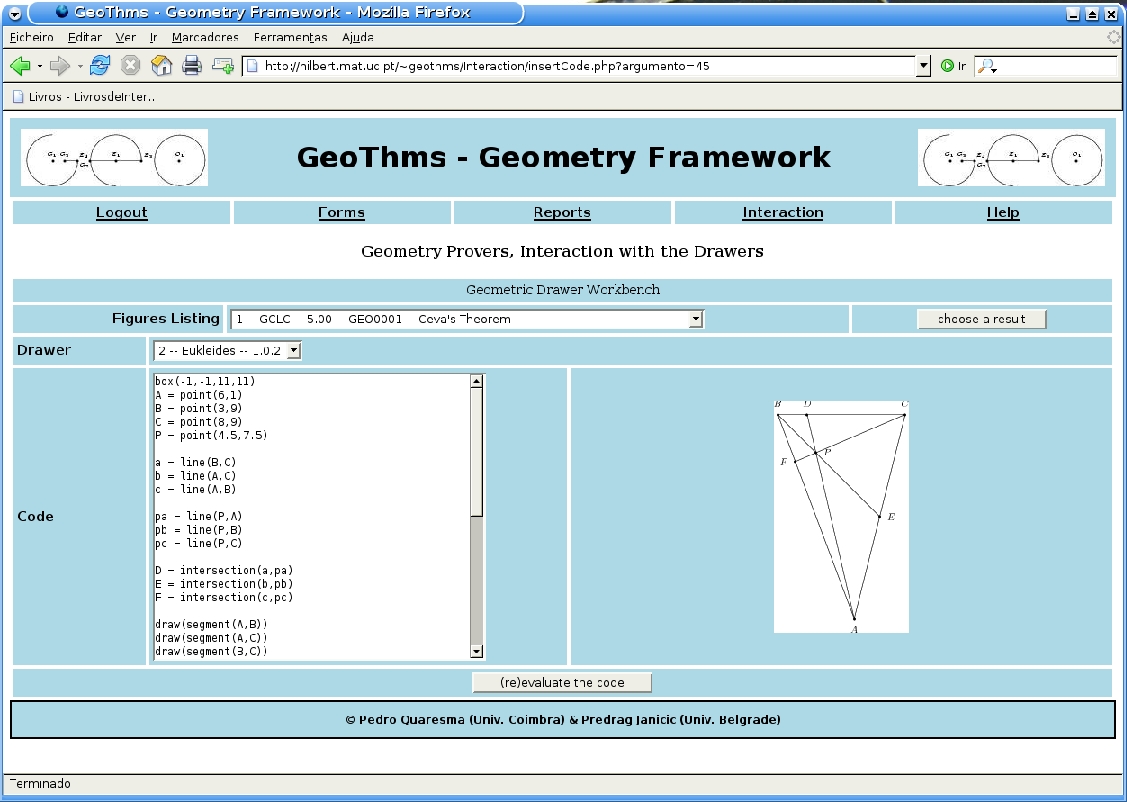
access to a second level (see Figure )
where he/she can browse the data from the database (see
Figure ), (in a formatted form, or in a
textual form) (see Figure ) and use the
drawing/proof tools in an interactive way (see
Figure ).
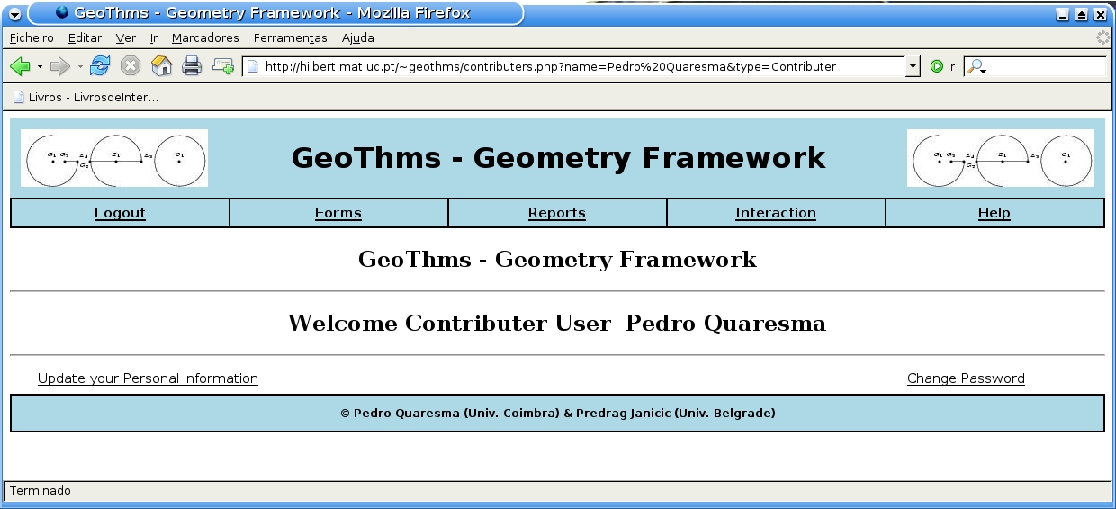
A regular user can apply to the status of contributer (see
Figure ) in which case he/she will have
the possibility to insert new data, and/or to update the data he/she
had inserted previously (see Figure ).
Constructions are described and stored in declarative languages of
dynamic geometry tools such as GCLC and Eukleides. Figures are
generated directly on the basis of geometric specifications, by GCLC
and Eukleides and stored as Jpeg files. Conjectures are described and
stored in a a form that extend geometric specifications. The
specifications of conjectures are used (directly or via a converter) by
GCLCprover. Proofs are generated by GCLCprover and stored as PDF
files (produced by LaTeX from the ATP output and using a specific
layout, specified by gclc_proof LaTeX style file).
The framework can be augmented by other dynamic geometry tools, and
other geometry theorem provers.
GeoThms gives the user a complex framework suitable for new ways of
communicating geometric knowledge, it provides an open system where
one can learn from the existing knowledge base and seek for new
results. GeoThms also provides a system for storing geometric
knowledge (in a strict, declarative form) -- not only theorem
statements, but also their (automatically generated) proofs and
corresponding figures, i.e., visualisations.
Pedro Quaresma and Predrag Janicic